複数辞典一括検索+![]()
![]()
広辞苑の検索結果 (1)
さんかく‐かんすう【三角関数】‥クワン‥🔗⭐🔉
さんかく‐かんすう【三角関数】‥クワン‥
直角三角形の直角でない1角の大きさをαとすると、この三角形の任意の2辺の長さの比は、この角αの大きさによって定まる。この比をこの角の三角比という。一つの角に対して6種類の三角比がある。これらをそれぞれ
PM/OP=sinα ,
OM/OP=cosα
,
OM/OP=cosα ,
PM/OM=tanα
,
PM/OM=tanα ,
OM/PM=cotα
,
OM/PM=cotα ,
OP/OM=secα
,
OP/OM=secα ,
OP/PM=cosecα
,
OP/PM=cosecα と記し、それぞれサイン(正弦)・コサイン(余弦)・タンジェント(正接)・コタンジェント(余接)・セカント(正割)・コセカント(余割)という。このαを一般角に拡張し、cosα,sinαなどをαの関数とみたとき、三角関数と総称する。すなわち単位円周上の点P(x,y)をOPとx軸のなす一般角αを用いて、x=cosα,y=sinαと表し、それぞれ余弦関数・正弦関数という。円関数。
三角関数
と記し、それぞれサイン(正弦)・コサイン(余弦)・タンジェント(正接)・コタンジェント(余接)・セカント(正割)・コセカント(余割)という。このαを一般角に拡張し、cosα,sinαなどをαの関数とみたとき、三角関数と総称する。すなわち単位円周上の点P(x,y)をOPとx軸のなす一般角αを用いて、x=cosα,y=sinαと表し、それぞれ余弦関数・正弦関数という。円関数。
三角関数
 ⇒さん‐かく【三角】
⇒さん‐かく【三角】
 ,
OM/OP=cosα
,
OM/OP=cosα ,
PM/OM=tanα
,
PM/OM=tanα ,
OM/PM=cotα
,
OM/PM=cotα ,
OP/OM=secα
,
OP/OM=secα ,
OP/PM=cosecα
,
OP/PM=cosecα と記し、それぞれサイン(正弦)・コサイン(余弦)・タンジェント(正接)・コタンジェント(余接)・セカント(正割)・コセカント(余割)という。このαを一般角に拡張し、cosα,sinαなどをαの関数とみたとき、三角関数と総称する。すなわち単位円周上の点P(x,y)をOPとx軸のなす一般角αを用いて、x=cosα,y=sinαと表し、それぞれ余弦関数・正弦関数という。円関数。
三角関数
と記し、それぞれサイン(正弦)・コサイン(余弦)・タンジェント(正接)・コタンジェント(余接)・セカント(正割)・コセカント(余割)という。このαを一般角に拡張し、cosα,sinαなどをαの関数とみたとき、三角関数と総称する。すなわち単位円周上の点P(x,y)をOPとx軸のなす一般角αを用いて、x=cosα,y=sinαと表し、それぞれ余弦関数・正弦関数という。円関数。
三角関数
 ⇒さん‐かく【三角】
⇒さん‐かく【三角】
大辞林の検索結果 (1)
さんかく-かんすう【三角関数】🔗⭐🔉
さんかく-かんすう ―クワン― [5] 【三角関数】
直角三角形の直角でない角の一つを θ とすると,三辺相互の比の値は θ により定まる。これを角 θ の三角比といい,図の場合 sin θ=BC/AB cos θ=AC/AB tan θ=BC/AC cot θ=AC/BC sec θ=AB/AC cosec θ=AB/BC と表し,それぞれ θ の正弦(サイン),余弦(コサイン),正接(タンジェント),余接(コタンジェント),正割(セカント),余割(コセカント)という。これらを角 θ の関数とみたとき,三角関数という。三角関数の概念は,θ が一般角の場合にも拡張される。すなわち,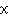
 座標において,点 P(
座標において,点 P(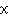 ,
,  )と原点 O との距離を
)と原点 O との距離を 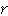 ,半直線 OP(動径)と
,半直線 OP(動径)と 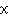 軸がなす角を θ とし,半直線 OP が回転するとき,図左に掲げたような
軸がなす角を θ とし,半直線 OP が回転するとき,図左に掲げたような 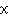 ,
, ,
,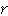 の比は θ の関数となる。この六種の関数を三角関数という。円関数。
三角関数
の比は θ の関数となる。この六種の関数を三角関数という。円関数。
三角関数
 [図]
[図]
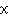
 座標において,点 P(
座標において,点 P(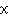 ,
,  )と原点 O との距離を
)と原点 O との距離を 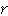 ,半直線 OP(動径)と
,半直線 OP(動径)と 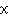 軸がなす角を θ とし,半直線 OP が回転するとき,図左に掲げたような
軸がなす角を θ とし,半直線 OP が回転するとき,図左に掲げたような 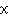 ,
, ,
,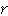 の比は θ の関数となる。この六種の関数を三角関数という。円関数。
三角関数
の比は θ の関数となる。この六種の関数を三角関数という。円関数。
三角関数
 [図]
[図]
広辞苑+大辞林に「三角関数」で始まるの検索結果。