複数辞典一括検索+![]()
![]()
広辞苑の検索結果 (5)
すう‐がく【数学】🔗⭐🔉
すう‐がく【数学】
①(mathematics)数量および空間に関して研究する学問。代数学・幾何学・解析学(微分学・積分学およびその他の諸分科)、ならびにそれらの応用などを含む。泉鏡花、三之巻「強しゐてまた―教うる私塾に塾生とはなれりしかど」
②数についての学問。すなわち今の算術(arithmetic)。中国の「数学啓蒙」(1853年刊)以来、日本でも明治10年代まで、この意味に用いたことが多い。
⇒すうがく‐オリンピック【数学オリンピック】
⇒すうがく‐きそろん【数学基礎論】
⇒すうがくてき‐きのうほう【数学的帰納法】
⇒すうがくてき‐ろんりがく【数学的論理学】
すうがく‐オリンピック【数学オリンピック】🔗⭐🔉
すうがく‐オリンピック【数学オリンピック】
世界各国の数学の得意な中学・高校生が集まり、その能力を競うとともに国際交流を促進する大会。1959年から毎年行われ、日本は90年から参加。
⇒すう‐がく【数学】
すうがく‐きそろん【数学基礎論】🔗⭐🔉
すうがく‐きそろん【数学基礎論】
数学の論理的構造を究明する科学。集合論から派生した逆理を解決するために発生し、記号論理学的方法を採る。
⇒すう‐がく【数学】
すうがくてき‐きのうほう【数学的帰納法】‥ナフハフ🔗⭐🔉
すうがくてき‐きのうほう【数学的帰納法】‥ナフハフ
〔数〕ある自然数nに関する命題が、⑴n=1について成立し、⑵任意の自然数kについて、その命題が成立すると仮定すれば、k+1についても成立すること、以上二つが証明されるならば、その命題はどんな自然数についても成立するという原理を用いた証明法。
⇒すう‐がく【数学】
すうがくてき‐ろんりがく【数学的論理学】🔗⭐🔉
すうがくてき‐ろんりがく【数学的論理学】
(→)記号論理学に同じ。
⇒すう‐がく【数学】
○数が知れるすうがしれる
(主として明治期に用いた。下に打消の語を伴うことが多い)程度がわかる。おしはかることができる。幸田露伴、天うつ浪「ほんとにお前は何処まで人に世話を焼かせるのだか数が知れない人だよ」
⇒すう【数】
大辞林の検索結果 (5)
すう-がく【数学】🔗⭐🔉
すう-がく [0] 【数学】
〔mathematics〕
古くは数に関する学問,すなわち算術の意。現在では数・量および空間に関して研究し,さらに抽象的な概念を扱う学問になっている。
すうがく-きそろん【数学基礎論】🔗⭐🔉
すうがく-きそろん [6] 【数学基礎論】
一九世紀末から二〇世紀初頭に表れた集合論の矛盾を解決するため,二〇世紀初頭に成立した数学の一分科。数学の論理的構造を,記号論理を用いて研究する。広く数学的諸研究の理論的基礎となる。
すうがく-てき-きのうほう【数学的帰納法】🔗⭐🔉
すうがく-てき-きのうほう ―キナフハフ [0] 【数学的帰納法】
自然数 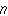 に関する命題において,(1)この命題が
に関する命題において,(1)この命題が 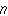 =1 のとき成立し,(2)
=1 のとき成立し,(2) 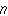 =
=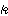 のとき成立すると仮定すれば
のとき成立すると仮定すれば 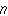 =
=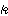 +1 のときにも成立する,という二つの事柄を証明できるとき,この命題はすべての自然数
+1 のときにも成立する,という二つの事柄を証明できるとき,この命題はすべての自然数 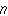 について成立する,と結論する証明法。
について成立する,と結論する証明法。
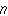 に関する命題において,(1)この命題が
に関する命題において,(1)この命題が 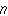 =1 のとき成立し,(2)
=1 のとき成立し,(2) 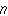 =
=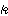 のとき成立すると仮定すれば
のとき成立すると仮定すれば 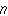 =
=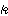 +1 のときにも成立する,という二つの事柄を証明できるとき,この命題はすべての自然数
+1 のときにも成立する,という二つの事柄を証明できるとき,この命題はすべての自然数 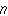 について成立する,と結論する証明法。
について成立する,と結論する証明法。
すうがく-てき-ろんりがく【数学的論理学】🔗⭐🔉
すうがく-てき-ろんりがく [9] 【数学的論理学】
記号論理学のこと。数学的推論(証明)の構造を形式化したものであることからの名。数理論理学。
→記号論理学
すうがく【数学】(和英)🔗⭐🔉
広辞苑+大辞林に「数学−」で始まるの検索結果。