複数辞典一括検索+![]()
![]()
広辞苑の検索結果 (9)
たい‐しょう【対称】🔗⭐🔉
たい‐しょう【対称】
(symmetry)
①互いに対応してつりあっていること。相称。
㋐〔数〕一定点Oを通る直線上で、Oに関しそれぞれ反対の側にあってOから等距離の2点を、Oに関し互いに対称な点といい、Oを対称中心という。また、ある直線lまたは平面αに対する垂線上で、lまたはαのそれぞれ反対側にあって、それらから等距離の2点を、lまたはαに関し互いに対称な点といい、lまたはαをそれぞれ対称軸または対称面という。図形上のすべての点の対称点がその図形自身に含まれるとき、この図形を対称な図形という。→線対称→面対称→点対称
㋑〔理〕結晶質物質において、結晶面あるいは原子・分子の間にある規則正しい関係の一種。一つの結晶面あるいは原子・分子を、ある他の面によって反射、またはある軸によって回転などした時に、他の結晶面あるいは原子・分子に一致する性質。
②代名詞の第二人称。
⇒たいしょう‐いどう【対称移動】
⇒たいしょう‐しき【対称式】
⇒たいしょう‐せい【対称性】
⇒たいしょう‐だいめいし【対称代名詞】
⇒たいしょう‐ちゅうしん【対称中心】
⇒たいしょう‐てき【対称的】
⇒たいしょう‐めん【対称面】
⇒たいしょう‐りつ【対称律】
たいしょう‐いどう【対称移動】🔗⭐🔉
たいしょう‐いどう【対称移動】
点または図形を、対称中心、対称軸、対称面の反対側に移動すること。→対称1㋐。
⇒たい‐しょう【対称】
たいしょう‐しき【対称式】🔗⭐🔉
たいしょう‐しき【対称式】
式の中のある2文字を交換しても値を変えない代数式。例a2+b2+c2
⇒たい‐しょう【対称】
たいしょう‐せい【対称性】🔗⭐🔉
たいしょう‐せい【対称性】
任意の物理系に平行移動・回転などの変換を行なっても系の物理的性質が変わらないこと。その変換を対称変換といい、その変換に対応する対称性があるという。不変性。
⇒たい‐しょう【対称】
たいしょう‐だいめいし【対称代名詞】🔗⭐🔉
たいしょう‐だいめいし【対称代名詞】
二人称を表す代名詞。
⇒たい‐しょう【対称】
たいしょう‐ちゅうしん【対称中心】🔗⭐🔉
たいしょう‐ちゅうしん【対称中心】
「対称1㋐」参照。
⇒たい‐しょう【対称】
たいしょう‐てき【対称的】🔗⭐🔉
たいしょう‐てき【対称的】
形や配列に対称がとれているさま。
⇒たい‐しょう【対称】
たいしょう‐めん【対称面】🔗⭐🔉
たいしょう‐めん【対称面】
「対称1㋐」参照。
⇒たい‐しょう【対称】
たいしょう‐りつ【対称律】🔗⭐🔉
たいしょう‐りつ【対称律】
〔数〕ある集合の任意の2元に対して定義された関係〜について、a〜bならばb〜aという関係。反射律・推移律とともに同値の概念を規定する。
⇒たい‐しょう【対称】
大辞林の検索結果 (8)
たい-しょう【対称】🔗⭐🔉
たい-しょう [0] 【対称】
(1)互いに対応してつりあうこと。相称。
(2)〔文法〕「二人称」に同じ。
(3)〔数〕
〔symmetry〕
(ア)(点対称)二点 P,Q が点 O に関して対称とは,この二点を結ぶ線分 PQ が O によって二等分されること。すなわち,P,Q は O を通る一つの直線上にあって,O に関して反対側で,O から等距離にあること。点 O を対称の中心という。(イ)(線対称)二点 P,Q が直線  に関して対称とは,線分 PQ が
に関して対称とは,線分 PQ が  によって垂直に二等分されること。
によって垂直に二等分されること。 を対称軸という。(ウ)(面対称)空間の二点 P,Q が平面αに関して対称とは,線分 PQ がαによって垂直に二等分されること。αを対称面という。(エ)(対称な図形)二点 P,Q が点 O に関して対称な時,Q を O に関する P の対称点といい,図形 F の点の,O に関する対称点全体のつくる図形を,O に関して F と対称な図形という。特に,図形 F の任意の点の,O に関する対称点がまた F の点である時,図形 F は点 O に関し対称であるという。線対称,面対称についても同様の言い方をする。平面図形の場合には,点 O に関して対称とは,O を中心として一八〇度回転すれば重なることであり,直線
を対称軸という。(ウ)(面対称)空間の二点 P,Q が平面αに関して対称とは,線分 PQ がαによって垂直に二等分されること。αを対称面という。(エ)(対称な図形)二点 P,Q が点 O に関して対称な時,Q を O に関する P の対称点といい,図形 F の点の,O に関する対称点全体のつくる図形を,O に関して F と対称な図形という。特に,図形 F の任意の点の,O に関する対称点がまた F の点である時,図形 F は点 O に関し対称であるという。線対称,面対称についても同様の言い方をする。平面図形の場合には,点 O に関して対称とは,O を中心として一八〇度回転すれば重なることであり,直線  に関して対称とは,
に関して対称とは, を折り目として折り返した時,重なることである。
(4)結晶で,ある直線上の一点,または一つの平面を隔てて回転・反射・逆転・回転反射などの操作を施しても,前と同じ面・頂点,稜などに一致すること。
を折り目として折り返した時,重なることである。
(4)結晶で,ある直線上の一点,または一つの平面を隔てて回転・反射・逆転・回転反射などの操作を施しても,前と同じ面・頂点,稜などに一致すること。
 に関して対称とは,線分 PQ が
に関して対称とは,線分 PQ が  によって垂直に二等分されること。
によって垂直に二等分されること。 を対称軸という。(ウ)(面対称)空間の二点 P,Q が平面αに関して対称とは,線分 PQ がαによって垂直に二等分されること。αを対称面という。(エ)(対称な図形)二点 P,Q が点 O に関して対称な時,Q を O に関する P の対称点といい,図形 F の点の,O に関する対称点全体のつくる図形を,O に関して F と対称な図形という。特に,図形 F の任意の点の,O に関する対称点がまた F の点である時,図形 F は点 O に関し対称であるという。線対称,面対称についても同様の言い方をする。平面図形の場合には,点 O に関して対称とは,O を中心として一八〇度回転すれば重なることであり,直線
を対称軸という。(ウ)(面対称)空間の二点 P,Q が平面αに関して対称とは,線分 PQ がαによって垂直に二等分されること。αを対称面という。(エ)(対称な図形)二点 P,Q が点 O に関して対称な時,Q を O に関する P の対称点といい,図形 F の点の,O に関する対称点全体のつくる図形を,O に関して F と対称な図形という。特に,図形 F の任意の点の,O に関する対称点がまた F の点である時,図形 F は点 O に関し対称であるという。線対称,面対称についても同様の言い方をする。平面図形の場合には,点 O に関して対称とは,O を中心として一八〇度回転すれば重なることであり,直線  に関して対称とは,
に関して対称とは, を折り目として折り返した時,重なることである。
(4)結晶で,ある直線上の一点,または一つの平面を隔てて回転・反射・逆転・回転反射などの操作を施しても,前と同じ面・頂点,稜などに一致すること。
を折り目として折り返した時,重なることである。
(4)結晶で,ある直線上の一点,または一つの平面を隔てて回転・反射・逆転・回転反射などの操作を施しても,前と同じ面・頂点,稜などに一致すること。
たいしょう-しき【対称式】🔗⭐🔉
たいしょう-しき [3] 【対称式】
式の中の任意の二つの文字を入れ替えても,その値が変わらない整式。例えば 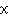
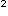 +
+
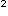 +
+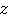
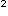 ,
, 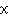
 +
+
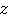 +
+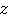
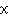 など。
など。
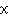
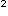 +
+
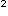 +
+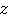
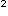 ,
, 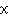
 +
+
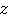 +
+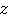
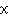 など。
など。
たいしょう-ずけい【対称図形】🔗⭐🔉
たいしょう-ずけい ―ヅ― [5] 【対称図形】
図形自身が点対称,あるいは線対称,あるいは面対称のもの。例えば平行四辺形(点対称),等脚台形(線対称),球(面対称)など。
たいしょう-せい【対称性】🔗⭐🔉
たいしょう-せい [0] 【対称性】
〔物〕 物理系に座標変換などの変換を行うとき,系を支配する基本法則の形が変わらなければ,系はその変換に対して,対称性あるいは不変性をもつという。対称性は物理量の保存則と強く結びついており,例えば,運動量,エネルギーの保存則は,それぞれ座標系の平行移動,時間のずらしに対する対称性に基づく。
たいしょう-だいめいし【対称代名詞】🔗⭐🔉
たいしょう-だいめいし [7] 【対称代名詞】
代名詞の一。話し手が聞き手を指し示すのに用いるもの。「あなた」「きみ」「なんじ」の類。二人称代名詞。
たいしょう-てき【対称的】🔗⭐🔉
たいしょう-てき [0] 【対称的】 (形動)
物の形や配列に対称がとれているさま。
たいしょう-りつ【対称律】🔗⭐🔉
たいしょう-りつ [3] 【対称律】
 =
=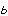 ならば
ならば 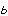 =
= という性質。
という性質。 が
が 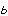 とある関係にあるならば,
とある関係にあるならば,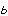 も
も  とその関係にあるということ。
とその関係にあるということ。
 =
=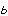 ならば
ならば 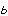 =
= という性質。
という性質。 が
が 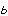 とある関係にあるならば,
とある関係にあるならば,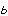 も
も  とその関係にあるということ。
とその関係にあるということ。
たいしょう【対称】(和英)🔗⭐🔉
たいしょう【対称】
symmetry.→英和
〜的 symmetrical.
広辞苑+大辞林に「対称」で始まるの検索結果。