複数辞典一括検索+![]()
![]()
広辞苑の検索結果 (3)
ぐん【群】🔗⭐🔉
ぐん【群】
①むらがり。むれ。あつまり。「―をなす」
②〔数〕(group)一つの集合があって、これを構成する要素(元という)の間に次の四つの条件を満たす一つの算法 が規定されているとき、この集合を群という。(ア)この集合の二つの元aとbに対してa
が規定されているとき、この集合を群という。(ア)この集合の二つの元aとbに対してa bもまたこの集合の元である。(イ)結合律a
bもまたこの集合の元である。(イ)結合律a (b
(b c)=(a
c)=(a b)
b) cが成り立つ。(ウ)単位元(すべての元aに対してe
cが成り立つ。(ウ)単位元(すべての元aに対してe a=a
a=a e=aが成り立つような元e)が含まれている。(エ)逆元(元aに対しa
e=aが成り立つような元e)が含まれている。(エ)逆元(元aに対しa x=x
x=x a=eが成り立つような元x)が含まれている。
⇒群を抜く
a=eが成り立つような元x)が含まれている。
⇒群を抜く
 が規定されているとき、この集合を群という。(ア)この集合の二つの元aとbに対してa
が規定されているとき、この集合を群という。(ア)この集合の二つの元aとbに対してa bもまたこの集合の元である。(イ)結合律a
bもまたこの集合の元である。(イ)結合律a (b
(b c)=(a
c)=(a b)
b) cが成り立つ。(ウ)単位元(すべての元aに対してe
cが成り立つ。(ウ)単位元(すべての元aに対してe a=a
a=a e=aが成り立つような元e)が含まれている。(エ)逆元(元aに対しa
e=aが成り立つような元e)が含まれている。(エ)逆元(元aに対しa x=x
x=x a=eが成り立つような元x)が含まれている。
⇒群を抜く
a=eが成り立つような元x)が含まれている。
⇒群を抜く
むら【群・叢・簇】🔗⭐🔉
むら【群・叢・簇】
(ムレの古形)群がること。また、そのもの。むれ。古事記下「かぎろひの燃ゆる家―」
[漢]群🔗⭐🔉
群 字形
 筆順
筆順
 〔羊(
〔羊(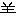 )部7画/13画/教育/2318・3732〕
〔音〕グン(呉) クン(漢)
〔訓〕むれる・むれ・むらがる・むら=
[意味]
①同類のものが多く集まる。むれる。むらがる。「群集ぐんしゅう・くんじゅ・群発」
②集まった仲間。むれ。「群を抜く」「鶏群の一鶴」「魚群・大群・抜群ばつぐん・ばっくん」
③多くの。もろもろの。「群雄・群臣・群小」
[解字]
形声。「羊」+音符「君」(=まるくまとまる)。羊のむれの意。[羣]は異体字。
)部7画/13画/教育/2318・3732〕
〔音〕グン(呉) クン(漢)
〔訓〕むれる・むれ・むらがる・むら=
[意味]
①同類のものが多く集まる。むれる。むらがる。「群集ぐんしゅう・くんじゅ・群発」
②集まった仲間。むれ。「群を抜く」「鶏群の一鶴」「魚群・大群・抜群ばつぐん・ばっくん」
③多くの。もろもろの。「群雄・群臣・群小」
[解字]
形声。「羊」+音符「君」(=まるくまとまる)。羊のむれの意。[羣]は異体字。
 筆順
筆順
 〔羊(
〔羊( )部7画/13画/教育/2318・3732〕
〔音〕グン(呉) クン(漢)
〔訓〕むれる・むれ・むらがる・むら=
[意味]
①同類のものが多く集まる。むれる。むらがる。「群集ぐんしゅう・くんじゅ・群発」
②集まった仲間。むれ。「群を抜く」「鶏群の一鶴」「魚群・大群・抜群ばつぐん・ばっくん」
③多くの。もろもろの。「群雄・群臣・群小」
[解字]
形声。「羊」+音符「君」(=まるくまとまる)。羊のむれの意。[羣]は異体字。
)部7画/13画/教育/2318・3732〕
〔音〕グン(呉) クン(漢)
〔訓〕むれる・むれ・むらがる・むら=
[意味]
①同類のものが多く集まる。むれる。むらがる。「群集ぐんしゅう・くんじゅ・群発」
②集まった仲間。むれ。「群を抜く」「鶏群の一鶴」「魚群・大群・抜群ばつぐん・ばっくん」
③多くの。もろもろの。「群雄・群臣・群小」
[解字]
形声。「羊」+音符「君」(=まるくまとまる)。羊のむれの意。[羣]は異体字。
大辞林の検索結果 (3)
ぐん【群】🔗⭐🔉
ぐん [1] 【群】
(1)多くの同類のものが集まっていること。むれ。むらがり。集まり。
(2)〔数〕
〔group〕
一つの集合において,その,元(要素)の間に算法,例えば乗法が定められ,(1)二つの元  ,
, 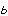 の積
の積  ・
・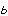 もその集合の元である(2)結合法則(
もその集合の元である(2)結合法則( ・
・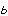 )・
)・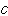 =
= ・(
・(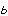 ・
・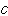 )が成り立つ(3)すべての元
)が成り立つ(3)すべての元  に対して
に対して  ・
・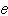 =
=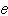 ・
・ =
= となる
となる 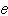 (単位元)が存在する(4)各元
(単位元)が存在する(4)各元  に対して
に対して  ・
・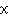 =
=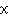 ・
・ =
=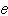 となる元
となる元 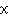 =
=

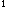 (逆元)が存在する,という四つの条件が満たされている時,この集合はその算法に関して群であるという。特に交換法則
(逆元)が存在する,という四つの条件が満たされている時,この集合はその算法に関して群であるという。特に交換法則  ・
・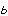 =
=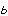 ・
・ が成り立つ群をアーベル群または可換群という。群の考えはフランスのガロアなどにより導入され,現代数学の大きな基礎となっている。
が成り立つ群をアーベル群または可換群という。群の考えはフランスのガロアなどにより導入され,現代数学の大きな基礎となっている。
 ,
, 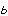 の積
の積  ・
・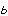 もその集合の元である(2)結合法則(
もその集合の元である(2)結合法則( ・
・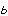 )・
)・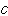 =
= ・(
・(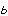 ・
・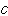 )が成り立つ(3)すべての元
)が成り立つ(3)すべての元  に対して
に対して  ・
・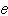 =
=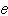 ・
・ =
= となる
となる 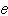 (単位元)が存在する(4)各元
(単位元)が存在する(4)各元  に対して
に対して  ・
・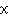 =
=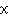 ・
・ =
=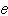 となる元
となる元 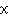 =
=

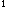 (逆元)が存在する,という四つの条件が満たされている時,この集合はその算法に関して群であるという。特に交換法則
(逆元)が存在する,という四つの条件が満たされている時,この集合はその算法に関して群であるという。特に交換法則  ・
・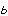 =
=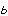 ・
・ が成り立つ群をアーベル群または可換群という。群の考えはフランスのガロアなどにより導入され,現代数学の大きな基礎となっている。
が成り立つ群をアーベル群または可換群という。群の考えはフランスのガロアなどにより導入され,現代数学の大きな基礎となっている。
むら【群・叢・簇】🔗⭐🔉
むら [2] 【群・叢・簇】
群がっていること。群がり。群れ。現代語では多く複合語として用いる。「稲―」「草―」
広辞苑+大辞林に「群」で完全一致するの検索結果。